Half Adder Using Basic Gates
Aim
To study and verify the Half Adder Using Basic Gates.Learning Objectives
- To understand the behavior and demonstrate Half Adder Using Basic Gates.
- To apply knowledge of the fundamental gates to create truth tables.
- To develop digital circuit building and troubleshooting skills.
- To understand key elements of TTL logic specification or datasheets.
IC Used
| IC Number | IC Name |
|---|---|
| 74LS08 | Quad 2-input AND Gates |
| 74LS86 | Quad 2-input Exclusive-OR Gates |
Circuit Tutorials:
Procedure
- Place the IC on IC Trainer Kit.
- Connect VCC and ground to respective pins of IC Trainer Kit.
- Implement the circuit as shown in the circuit diagram.
- Connect the inputs to the input switches provided in the IC Trainer Kit.
- Connect the outputs to the switches of O/P LEDs
- Apply various combinations of inputs according to the truth table and observe the condition of LEDs.
- Note down the corresponding output readings for various combinations of inputs.
- Power Off Trainer Kit, disconnect all the wire connections and remove IC's from IC-Base.
Theory
HALF ADDER - An adder is a digital logic circuit in electronics that implements the addition of numbers. In many computers and other types of processors, adders are used to calculate addresses, similar operations and table indices in the ALU and also in other parts of the processors. These can be built for many numerical representations like excess-3 or binary coded decimal. Adders are classified into two types: half adder and full adder. The half adder circuit has two inputs: A and B, which add two input digits and generate a carry and sum.
An adder is a digital circuit that performs addition of numbers. The half adder adds two binary digits called as augend and addend and produces two outputs as sum and carry; XOR is applied to both inputs to produce sum and AND gate is applied to both inputs to produce carry.
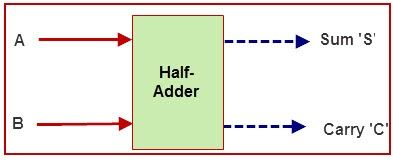
By using half adder, you can design simple addition with the help of logic gates. A half adder is used to add two single-digit binary numbers and results into a two-digit output. It is named as such because putting two half adders together with the use of an OR gate results in a full adder. In other words, it only does half the work of a full adder.
AND GATE - It is a digital circuit that has two or more inputs and produces an output, which is the logical AND of all those inputs. It is optional to represent the Logical AND with the symbol ‘.’
Logic AND Gates are available using digital circuits to produce the desired logical function and is given a symbol whose shape represents the logical operation of the AND gate. Because the Boolean expression for the logic AND function is defined as (.), which is a binary operation, AND gates can be cascaded together to form any number of individual inputs. However, commercial available AND gate IC’s are only available in standard 2, 3, or 4-input packages. If additional inputs are required, then standard AND gates will need to be cascaded together to obtain the required output value.
Boolean Expression Y = A.B
"If A and B is true, then Y is true"
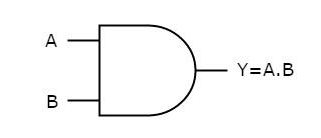
This AND gate produces an output Y, which is the logical AND of two inputs A, B.
Ex-OR GATE - The full form of Ex-OR gate is Exclusive-OR gate. Its function is the same as that of OR gate except for some cases, when the inputs having an even number of ones.
In other words, the output of an Exclusive-OR gate ONLY goes “HIGH” when its two input terminals are at “DIFFERENT” logic levels with respect to each other. The Exclusive-OR Gate function, or Ex-OR for short, is achieved by combining standard logic gates together to form more complex gate functions that are used extensively in building arithmetic logic circuits, computational logic comparators and error detection circuits.
The two-input “Exclusive-OR” gate is basically a modulo two adder, since it gives the sum of two binary numbers.
Boolean Expression Y = A.B' + 'A.B = (A ⊕ B)
"If inputs having an odd number of ones, then Y is true"
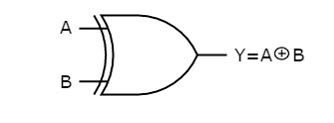
Ex-OR gate operation is similar to that of OR gate, except for a few combinations of inputs. The output of Ex-OR gate is ‘1’ when an odd number of ones present at the inputs. Hence, the output of Ex-OR gate is also called as an odd function.
Block Diagram
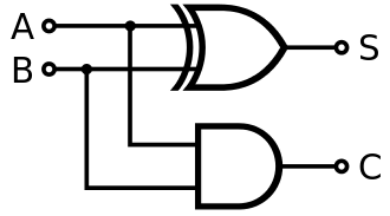
Precautions
- Make the connections according to the IC pin diagram.
- The connections should be tight on trainer kit.
- The Vcc and ground should be applied carefully at the specified pin only.
Conclusion
We have learned the Half Adder Using Basic Gates.Recommendations
Half Adder using NAND Gates
Aim: To study and verify the Half Adder using NAND Gates.
ICs used: 74LS00 Half Subtracter Using NAND Gates
Aim: To study and verify the Half Subtracter using NAND Gates.
ICs used: 74LS00 Full Subtractor using Two half adders basic gates
Aim: To study and Verify the Full Subtractor using Two half adders basic gates.
ICs used: 74LS8674LS0474LS0874LS32 Full Adder function using 3:8 Decoder
Aim: To study and Verify the Full Adder function using 3:8 Decoder.
ICs used: 74LS13874LS20 Half subtractor using basic gates
Aim: To study and Verify the Half subtractor using basic gates.
ICs used: 74LS8674LS0474LS08